紙に地図を描くとき、球体である地球を平面上に描くことになります。
平面上では距離・方位・面積・角度の全てを正しく表すことはできず、どこかにひずみが生じます。
そのため、利用方法によって様々な地図が用いられてきました。
その中でも特によく出てくる正距方位図法とメルカトル図法について紹介します。
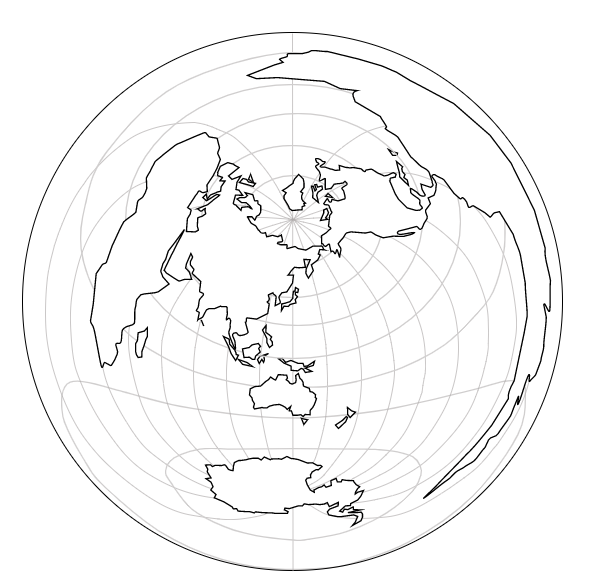
正距方位図法
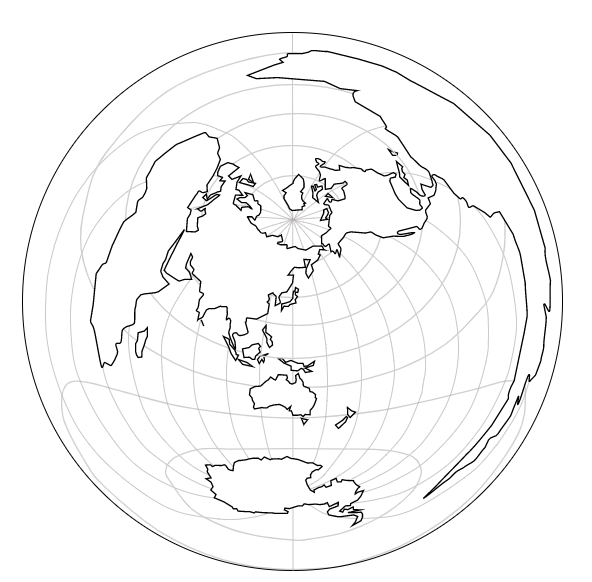
正距方位図には図の中心が存在します。
この地図では東京が中心になります。
名前からもわかるように、
図の中心(東京)と他の地点を結んだ直線の距離と方位が正しくなります。
図の中心を結んでいない直線は正しく表記できないので注意してください。
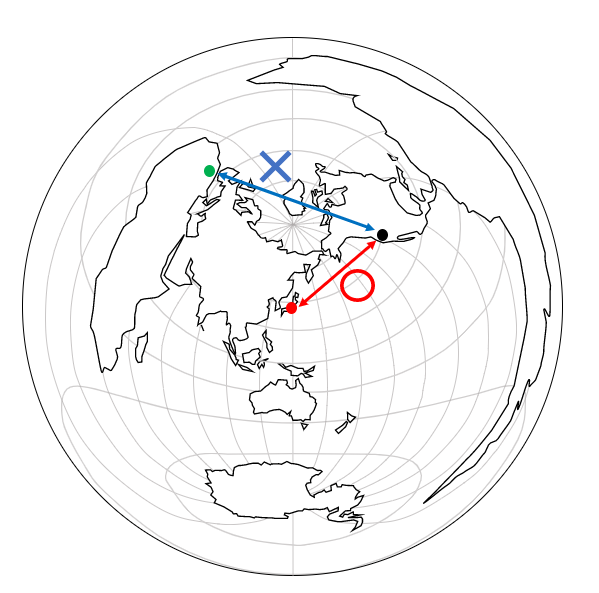
図の中心から引かれた直線は距離が正しい、
つまり最短距離を表しています。
この最短距離を示す直線を大圏航路(大圏コース)だったり、
大円コースと呼ばれています。
ちなみにこの地図は世界全体が描かれてるとして、
円の縁にあたるところは図の中心から何㎞あるでしょうか?
円の縁は図の中心から最も離れた地点であり、
地球上で正反対の位置する地点を示しています。
この地点を対蹠点とよびます。
もうおわかりかと思いますが、地球は1周4万㎞ですので、答えは2万㎞になります。
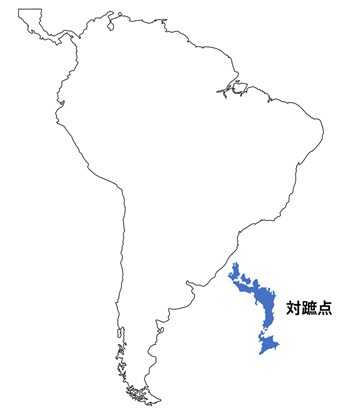
補足ですが、円の縁は全て対蹠点であり、同じ地点を示しています。
東西南北どこの方角から2万㎞進んでも、最後は地球の裏側にたどり着くという訳です。
このように地球の裏側になる地点を対蹠点といって、東京の対蹠点はアルゼンチン沖になります。
メルカトル図法
続いて緯線と経線が直角に交わるメルカトル図です。
この図は角度が正しい正角図法になります。
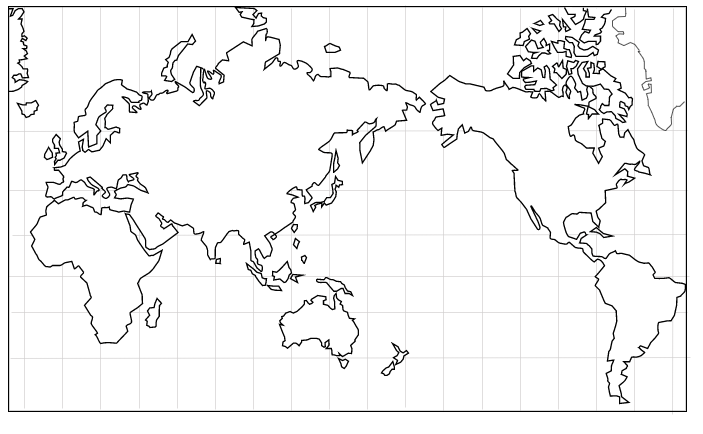
方位とは東西南北を意味しますが、角度とは正しいということはどういうことでしょうか?
それは2地点を結んだ直線が経線または緯線と交わったとき、
地球上での実際の角度と同じになるということです。
この2地点間を結んだ直線を等角航路と呼びます。
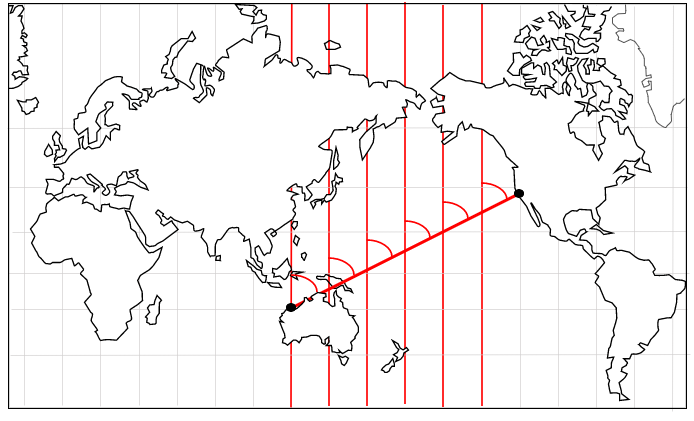
しかし、等角航路は最短距離ではありません。
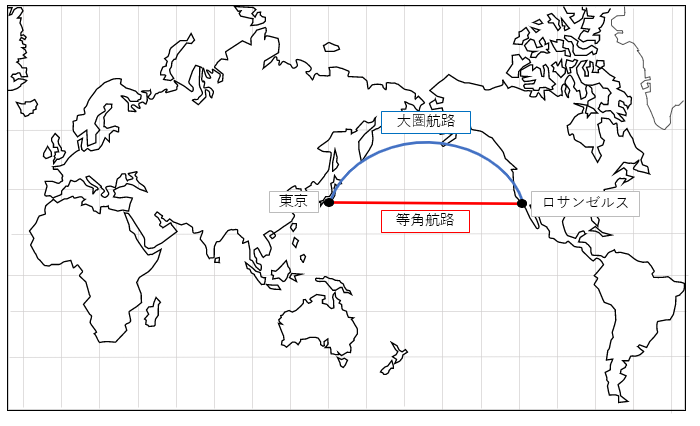
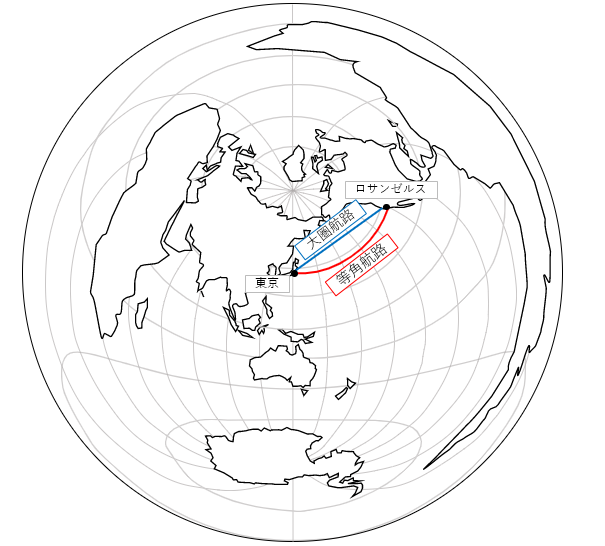
メルカトル図で大圏航路(最短距離)を表すと曲線になります。
下のメルカトル図と正距方位図を見比べてもらうと、
メルカトル図では最短距離が曲線で描かれるのも納得できるのではないでしょうか?
(大圏航路は北半球では上にカーブ、南半球では下にカーブします)
メルカトル図の直線は最短距離にはなりませんが、進行方向と経線の角度を一定に保つため、
現在でも海図に利用されています。
メルカトル図には問題点もあります。
ゆがみがないように思えますが、高緯度地域になるほど距離と面積が拡大されます。
赤道は一周4万㎞ですが、緯度60°では2万㎞になります。
地球一周分の長さは緯度によって変わるのです。
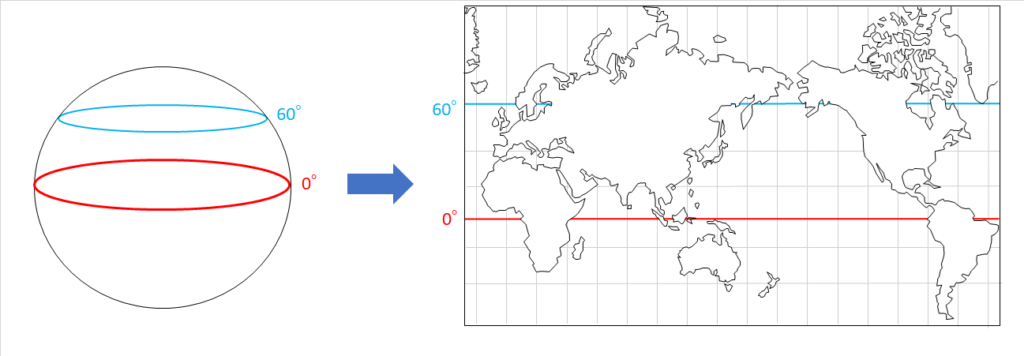
メルカトル図では緯線は全て同じ長さで描かれるので、実際の距離よりも長くなっています。
距離が長くなれば、面積も当然ひずみが生じて高緯度側は大きく描かれています。
一例としてオーストラリアよりもグリーンランドのほうが拡大して描かれていますが、
実際の面積はオーストラリアのほうが大きいです。
コメント